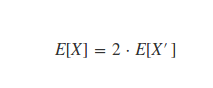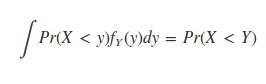دو مساله
دو مساله از دوره نظریه بازی ها میگذارم اینجا با حل خودم !
۱ . حالت ساده : نقطه ثابت براور
اگه نقشه ایران با مقیاس k رو بندازیم تو اتاق یه نقطه هست که رو خودش دقیقن می افته .
خب می گم اون تیکه اتاق که زیر نقشه است رو در نظر بگیر . حالا فرض من اصن نقشه همون تیکه هه اس و دو بازه اون تیکه ای که زیر نقشه است و در نطر بگیر و ... این طوری هر دفعه مساحت نقشه ضربدر مقیاس قزبدر مساخت نقشه می شه که قطعن از یک کم تره و در نهایت به صفر میل می کنه . پس اون مساحت که به صفر میل می کنه روی خودشه و خب اون یه نقطه اس.
الان نمی دونم این درسته یا نه ؟ چون اشاره ای به این که نقشه صرفن چرخش کرده و اندازه اش عوض شده به طور مستقیم نکردم و زیادی ساده اس.
۲ . تعادل تش ترکیبی برتراند
من دقیقن نمی دونم توی تعادل ترکیبی باید چی کار کنیم . اصل بی تفاوتی رو فضای پیوسته ی تابع چگالی معنی اش چی میشه رو نمی دونم.
چیزی که به دهنم رسید اول این بود که تابع چگالی رو هی فشرده اش کنم به سمت صفر و بگم بهتره . تا برسم به استراتژی محض صفر.
اگر تعادل نشی غیر از صفر موجود باشه و اسم استراتژی ما s باشه . یه استراتژی دیگه در نظر می گیریم که برابر با نیمه فشرده کردن s باشه:
f′x(x) = fx(2x)
اگر استراتژی قبلی به طور متوسط تی رو انتخاب کنه استراتژی جدید به طور متوسط تی دوم رو انتخاب می کنه
سود حاصل از استراتژی اول 100t-100t^2
سود حاصل از استراتژی دوم 50t-2.5t^2
50t-2.5t^2 > 1/2(100t-10t^2) =50t-5t^2
پس کافیه ثابت کنم احتمال برد استراتژی دوم دست کم دو برابر احتمال برد استراتژی اوله
برای اینکار سعی کردم احتمال X < Y اگه 'X متغیری با چگالی دوم و X متعیری با چگالی اول باشه پیدا کنم .
این تیکه رو ببخشین از یه ابزار آنلاین استفاده کردم و بلاگ بیان هم دردسر داره تو عکس گذاشتن
تو خط سوم اون X عه .نه X' اشتباه شده.
که متاسفانه این درست نیس . این تلاش بی نتیجه موند.
یعنی به نطرم اون حالتی که بی نتیجه موند جایی بود که طرف مقابل یه چگالی قطعه قطعه انتخاب کرده باشه . خب به ازای هر قطعه ما اگه با احتمال ابن قطعه یه اپسیلون کم تر رو انتخاب کنیم قطعا ضرر نمی کنیم:) شهودم می گه توی هر قطعه به جای این که یه چگالی از اون قطعه برداریم یه اپسلون کم ترش رو انتخاب کنیم و خب به جز صفر که کمتر نداره برا بقیه نقاط این حرف درسته جدی:)
این تیکه دارم روی بازی حرف می زنم : حس می کنم طرف مقابل نمیاد قطعه قطعه انتخاب کنه و حتمن یه بازه پیوسته منتهی به صفر رو انتخاب می کنه . حالا که اون حتمن صفر رو انتخاب می کنه چرا ما نکنیم:D .حالا شاید اون ایده فشرده کردن استقرایی جواب بده .
شاید اون که نتونستم احتمال برد ۱/۲ رو ثابت کنم درست بوده و من نتونستم . شاید هم باید یه چگالی دیگه انتخاب کنم که خودش همین شرطو تو خودش داشته باشه .
آها فهمیدم تابع چگالی g رو از f می سازیم این طوری که توزیع تجمعی G=2F
خب پس احتمال این که g کم تر از k باشه 2 برابر اینه که f کم تر باشه حله .
الان پس استراتژی با چگالی g یهتر از f عه و خب اندازه بازه ای که g بین صفر و یکه نصف اندازه بازه ایه که f بین صفر و یکه . پس این کار رو حد بهش بدی همون استراتژی محض صفر می شه و تمام:)
